Chapter 12: Vector Valued Functions
Section 12.1 Vector Valued Functions and Curves in Space
From our text, we have:
Definition: A vector-valued function is a rule that assigns a vector to each input number. Typically a vector-valued function has the form
where x, y and z are scalar-valued functions.
The domain consists of those \(t\) in the domain of x, y, and z.
So the range is a collection of vectors.
Below is an example of a vector valued function plotted in Sage:
t = var('t')
# Define the tuple or vector
r = (cos(t), sin(t), t)
# Use parametric_plot3d for curves
# Syntax: parametric_plot3d( (x, y, z), (variable, start, end) )
parametric_plot3d(r, (t, 0, 6*pi), thickness=2).show(aspect_ratio=(4,4,1))
t = var('t')
f1 = 4 - 2*t
f2 = 2 - t
r2 = vector((t, f1, f2))
parametric_plot3d(r2, (t, 0, 2), thickness=2).show()
Limits
The limit of a vector valued function (so it appears) is also a vector:

We can’t find such limits directly in sage, but we can write a function to do it easily:
# Do assignment 12.1 with our new function
t = var('t')
V = vector([4*t^2 - t - 2, (t^2 + 2*t -63)/(t-7), 2*cos(t)])
latex(V)
\left(4 \, t^{2} - t - 2,\,\frac{t^{2} + 2 \, t - 63}{t - 7},\,2 \, \cos\left(t\right)\right)
def vvf_limit(fn, v, a):
"""Returns a list with the limit of a vector valued function
Parameters:
fn: The vector, list, or tuple representing the vector valued function
v: The variable used in the function
a: The "endpoint" or target of the limit, e.g. oo for infinity, 0, etc.
Returns:
A list of values with the limit of each component of the function
"""
l = list(fn)
return [limit(x, v, a) for x in l]
t = var('t')
r5 = [cos(t), sqrt(4 + t), 3*e**(2*t)]
print(vvf_limit(r5, t, 0))
[1, 2, 3]
%display plain
t = var('t')
x(t) = 4*t^2 - t -2
y(t) = (t^2 + 2*t -63)/(t-7)
z(t) = 2 * cos(t)
V = [x(t), y(t), z(t)]
print("12.1 question 5")
print(V)
print(vvf_limit(V, t, 7))
print("\n12.1 question 5")
V2 = [2*t^2 + 3*t -1, (t^2 + 2*t -24)/(t-4), 4*cos(t)]
print(V2)
vvf_limit(V2, t, 4)
lim(sin(t)/t, t, 0)
12.1 question 5
[4*t^2 - t - 2, (t^2 + 2*t - 63)/(t - 7), 2*cos(t)]
[187, 16, 2*cos(7)]
12.1 question 5
[2*t^2 + 3*t - 1, (t^2 + 2*t - 24)/(t - 4), 4*cos(t)]
1
Continutity
A vector valued function \(r(t)\) is continuous at \(t_0\) if \(\lim\limits_{t \to t_0} r(t) = r(t_0)\)
# An ellipse and an eliptical helix, comment out one or the other
x = var('x')
# parametric_plot([sin(x), 2*cos(x)], (x, 0, 2*pi))
parametric_plot3d([sin(x), 2*cos(x), x], (x, 0, 8*pi))
# Sustitution example:
r5(t) = [cos(t), sqrt(4 + t), 3*e**(2*t)]
print(r5(9), N(r5(9)))
(cos(9), sqrt(13), 3*e^18) (-0.911130261884677, 3.60555127546399, 1.96979907411992e8)
# 1. Import the Cylinder shape
from sage.plot.plot3d.shapes import Cylinder
# 2. Create the cylinder object: Cylinder(radius, height)
C = Cylinder(1, 2, color='blue', opacity=0.4)
# 3. Display the graph
C.show(aspect_ratio=(1,1,1))
# aspect_ratio=(1,1,1) ensures the axes are scaled equally, so it looks circular
Section 12.2 - The Derivative of vector-valued functions
The derivative of a vector valued function is simply the derivative of each component, so as in the case of limits, we can implement a function to find one easily in Sage.
def vvf_diff(fn, v, diff_n=1):
"""Returns a list representing the limit of a vector valued function
Parameters:
fn : The vector, list, or tuple representing the vector valued function
v : The variable used in the function
diff_n : 1 for first derivative, 2 for second, etc.
Returns:
A list of values with the limit of each component of the function
"""
l = list(fn)
return vector([diff(x, v, diff_n) for x in l])
# Test out the vvf_diff function
var('x')
V = vector([x^3 + 3*x, ln(x), 5*x + 3])
V_prime = vvf_diff(V, x)
assert V_prime.list() == [3*x^2 + 3, 1/x, 5]
print(V_prime)
(3*x^2 + 3, 1/x, 5)
# Solve a problem (12.2, q 3):
t = var('t')
print("Problem 12.2, q 3")
V = vector([-3*t^5 - 2, 4*e^(3*t), -5*sin(-3*t)])
print(V)
print(vvf_diff(V, t))
print("\nProblem 12.2, q 4")
V = vector([(-4)/(-t+6), (2*t)/(3*t^2 + 1), (-t^2)/(-7*t^3 - 2)])
print(V)
print(vvf_diff(V, t))
print("\nProblem 12.2, q 5 (second derivative)")
V = vector([6*t + 3*sin(t), 5*t + 6*cos(t)])
print (V)
print(vvf_diff(V, t, 2))
print(vvf_diff(vvf_diff(V, t), t))
Problem 12.2, q 3
(-3*t^5 - 2, 4*e^(3*t), -5*sin(-3*t))
(-15*t^4, 12*e^(3*t), 15*cos(-3*t))
Problem 12.2, q 4
(4/(t - 6), 2*t/(3*t^2 + 1), t^2/(7*t^3 + 2))
(-4/(t - 6)^2, -12*t^2/(3*t^2 + 1)^2 + 2/(3*t^2 + 1), -21*t^4/(7*t^3 + 2)^2 + 2*t/(7*t^3 + 2))
Problem 12.2, q 5 (second derivative)
(6*t + 3*sin(t), 5*t + 6*cos(t))
(-3*sin(t), -6*cos(t))
(-3*sin(t), -6*cos(t))
Velocity/Acceleration of Vector Valued Functions
In either \(\mathbb{R}^2\) or \(\mathbb{R}^3\) if a vector-valued function, \(r(t)\) represents the curve of position (e.g. at point \(t\)), then \(v(t) = r^{\prime}(t)\) is the velocity, and \(r^{\prime\prime}(t)\) is the acceleration. The speed is given by the magnitude of the velocity vector, \(\|v(t)\|\).
To do this in code, see the following example based on functions we’ve already defined.
# Find the velocity vector and speed given a position vector
# Our results agree with the example shown in the Video assignment 12.2 Q4, so they are correct,
# but the simplification on the speed value leaves room for improvement.
t = var('t')
pos_vector = vector([cos(pi * t), sin(pi*t), t^2/2])
velocity_vector = vector(vvf_diff(pos_vector, t)) # Need to wrap list in a vector again for "norm"
acceleration_vector = vvf_diff(pos_vector, t, 2)
speed = velocity_vector.norm().simplify()
print(velocity_vector)
print(acceleration_vector)
print(speed)
(-pi*sin(pi*t), pi*cos(pi*t), t)
(-pi^2*cos(pi*t), -pi^2*sin(pi*t), 1)
sqrt(pi^2*cos(pi*t)^2 + pi^2*sin(pi*t)^2 + t^2)
The Unit Tangent Vector.
A unit tangent vector for a VVF, \(r(t)\) is given by the derivative of the vector over the magnitude of that derivative. (So it’s similar to the formula for a unit vector.)
That is, assuming \(r^{\prime}(t) \ne 0\),
Calculating and Plotting a Unit Tangent Vector in SageMath
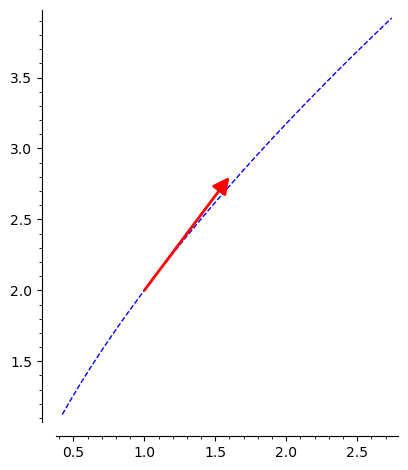
Let’s calculate one for \(r(t) = \langle t^3, 2t^2\rangle\), with a tangency point at t = 1. We get the correct values, but this vector would need to be graphed with the origin at the tangency point, (1,2). W
# Set up the curve
t = var('t')
r = vector([t**3, 2*t^2])
# Get the derivative, and plug in the point at which we want to draw the unit tangent vector
r_prime = vector(vvf_diff(r, t))
tangency_point = r(t=1)
print("Tangency point: ", tangency_point)
# Calculate the tangent vector using the formula above
tangent_vector = r_prime/r_prime.norm()
print("Tangent vector:", tangent_vector(t=1))
# Get a plot for the curve
plt = parametric_plot(r, (t, .75, 1.4), linestyle="dashed")
# Plot the unit tangent vector. By setting start equal to our tangency point, we place
# the vector tail where it belongs
plt2 = plot(tangent_vector(t=1), start=tangency_point, color="red")
plt += plt2
plt.show(aspect_ratio=1)
Tangency point: (1, 2)
Tangent vector: (3/5, 4/5)
A SageMath Function to get the Unit Tangent Vector
Since we’ll need it again below for a curvature problem, let’s implement a function to find a unit tangent vector:
def vvf_unit_tangent_vector(vec, var):
""" gets a unit tangent vector for the vector vec defined in terms of the variable var"""
r_prime = vector(vvf_diff(r, var))
return r_prime/r_prime.norm()
t = var('t')
r = vector([t**3, 2*t^2])
print(vvf_unit_tangent_vector(r, t))
(3*t^2/sqrt(9*abs(t)^4 + 16*abs(t)^2), 4*t/sqrt(9*abs(t)^4 + 16*abs(t)^2))
Anti-Derivatives: Integration of Vector Valued Functions
Given our discussion of limits and derivatives, we might have guessed that the integral of a vector valued function is calculated by taking the integral of each of the components. Thus, for example, given an indefinite integral for \(r(t) = \langle f(t), g(t), h(t)\rangle\), then the definite integral is as follows:
For the definite integral, we have: $\( \begin{aligned} \int_{a}^{b} \mathbf{r}(t) \, dt = \left( \int_{a}^{b} f(t) \, dt \right) \mathbf{i} + \left( \int_{a}^{b} g(t) \, dt \right) \mathbf{j} + \left( \int_{a}^{b} h(t) \, dt \right) \mathbf{k} \end{aligned} \)$
As we did before for limits and derivatives, we can easily implement this in sage
def vvf_integrate(fn, v, limits=None):
"""Returns a list with the integral of each component of a vector-valued function
Parameters:
fn: The vector, list, or tuple representing the vector valued function
v: The variable used in the function
limits: Either none or a two-element iterable for a definite integral.
Returns:
A list of values with the limit of each component of the function
Notes:
Initial condition problems are not yet handled by this function.
"""
l = list(fn)
if limits is None:
return [integrate(x, v) for x in l]
else:
return [integrate(x, v, limits[0], limits[1]) for x in l]
t = var('t')
r5 = [cos(t), sqrt(4 + t), 3*e**(2*t)]
# Test it out
print(vvf_integrate(r5, t))
print(vvf_integrate(r5, t, (0, pi/2)))
[sin(t), 2/3*(t + 4)^(3/2), 3/2*e^(2*t)]
[1, 2/3*(1/2*pi + 4)^(3/2) - 16/3, 3/2*e^pi - 3/2]
# Solve some problems with it. Let's start with 12.2, Q6
t = var('t')
r = vector([-4*t^2 + 1, -1*e^(-1 * t), 5 * sin(-4*t)])
print("12.2 Q6", vvf_integrate(r, t))
print("\nAdd initial conditions manually\nto each term for the next problem:")
r = vector([3 + 4*t, cos(t), 6*e^(3*t)])
print("\t12.2 Q7", vvf_integrate(r, t))
12.2 Q6 [-4/3*t^3 + t, e^(-t), 5/4*cos(4*t)]
Add initial conditions manually
to each term for the next problem:
12.2 Q7 [2*t^2 + 3*t, sin(t), 2*e^(3*t)]
diff(ln(2*t))
1/t
# Solving 12.2 Q9. We're asked to find the angle of
# intersection between two vectors. Originally I though we could just
# use get_angle_between_vectors with respect to the two vectors "as is",
# but it turns out we needed the angle between the tangent vectors
# of each funciton, so get the derivative first.
# Copied from another notebook -- at some point this needs to be a library!
def get_angle_between_vectors(v: vector, w: vector):
"""returns the angle between two vectors in radians."""
cos_theta = (v*w)/(v.norm() * w.norm())
return acos(cos_theta)
r1 = vector([2*t, t^3, -1*t^4])
r2 = vector([sin(-2 * t), sin(2*t), t - pi])
angle_as_fn = get_angle_between_vectors(diff(r1, t), diff(r2, t))
print(N(angle_as_fn(t=0)))
2.30052398302186
Solving another unit tangent vector problem
Question 12.2 # 10 asks us to find the unit tangent vector at the point \(t = 0\) for the function \(r(t) = \langle 4t^5 -2, -2 e^{3t}, -2 sin(5t) \rangle\)
Let’s do this using the technique we developed earlier:
# Set up the curve
t = var('t')
r = vector([4*t^5 - 2, -2*e^(3*t), -2 * sin(5*t)])
print(r)
# Get the derivative, and plug in the point at which we want to draw the unit tangent vector
r_prime = vector(vvf_diff(r, t))
tangency_point = r(t=0)
print("Tangency point: ", tangency_point)
# Calculate the tangent vector using the formula above
tangent_vector = r_prime/r_prime.norm()
print("Unit tangent vector:", tangent_vector(t=0))
(4*t^5 - 2, -2*e^(3*t), -2*sin(5*t))
Tangency point: (-2, -2, 0)
Unit tangent vector: (0, -3/34*sqrt(34), -5/34*sqrt(34))
Solving Some Velocity and Acceleration Vector Problems
12.2 question 11:
Given the vector function \(\mathbf{r}(t) = \left< -3t, \ -5t^3, \ -t^2 + 5 \right>\)
Find the velocity and acceleration vectors at \(t = -2\)
In our solution, below, we are finding derivatives as needed using vvf_diff. We don’t have a way to substitute into a whole vector (as far as I know), so we use a for comprehension in which we substitute each term to arrive at the correct vector.
t = var('t')
pos = r = vector([-3*t, -5*t^3, -t^2 + 5])
# print(r)
vel = vvf_diff(pos, t)
# print(vel)
accel = vvf_diff(vel, t)
# print(accel)
vel_at_minus_two = [x(t=-2) for x in vel]
accel_at_minus_two = [x(t=-2) for x in accel]
print("velocity at -2", vel_at_minus_two)
print("acceleration at -2", accel_at_minus_two)
velocity at -2 [-3, -60, 4]
acceleration at -2 [0, 60, -2]
Working with Initial Values
Question 12 asks us to find the anti-derivative of the acceleration function given initial condition for both our velocity and acceleration. Since our vvf_integrate function doesn’t handle initial conditions.
My first attempt at this problem failed, as shown in this Gemini session where I checked my work. To solve it correctly, I decided to capture the correct procedure that Gemini used by writing a SageMath function (yes, mine, not Gemini’s – I do some thinking here after all).
Here is the problem and the solution:
Find the position vector for a particle with acceleration, initial velocity, and initial position given below.
12.2 Question 12:
We’re asked to find \(\mathbf{r}(t)\).
Note, my first attempt at this was rather naive, adding the initial values to each expression. What’s really needed is for each term, \(n \in [0,2] \) of the velocity vector, for example:
Solve for \(V(t=0) + C_n = intial_values[n]\)
# Let's begin with our acceleration vector,
# integrate it, and "add" the v(0) initial condition as a vector
def vvf_initial_values(vec, var, init_val, init_val_equals):
""" Given an integral of a function in vec, returns a function based on initial values.
This involved solving for the constant of integration for each term.
Parameters:
vec: a function representing an indefinite integral of a vector_valued_function
var: the variable to substitute the initial_val
init_val: the initial variable
init_val_equals: a list of results for the function vec at the init_val
Returns:
a vector with the consants of integration adjusted appropriately
"""
# Result vector we'll be building.
init_values_solved = []
# Constant names
C = SR.var("C1, C2, C3")
for i in range(0, len(vec)):
# Start building the term for this "component" of the vector
# based on subtituting the initial value
substituted = (vec[i]).subs({var: init_val})
# Using the result, solve for constant of integration and add it to the
# component we're working on.
val = solve(substituted + C[i] - init_val_equals[i], C[i])[0]
init_values_solved.append(vec[i] + val.rhs())
return init_values_solved
# Work problem 12.2 # 12
t = var('t')
A = vector([6*t, 4*sin(t), cos(5*t)])
# Integrate the velocity vector, V, then modify it to V_0 based on the initial conditions
V = vector(vvf_integrate(A, t))
print("V: ", V)
V_0 = vvf_initial_values(V, t, 0, [-3, 4, 3])
print("V_0: ", V_0)
# Do the same for the acceleration vector
R = vector(vvf_integrate(V_0, t))
print("R: ", R)
R_0 = vvf_initial_values(R, t, 0, [2, -2, 4])
print("R_0: ", R_0)
print("At this point R_0 contains our final answer.")
V: (3*t^2, -4*cos(t), 1/5*sin(5*t))
V_0: [3*t^2 - 3, -4*cos(t) + 8, 1/5*sin(5*t) + 3]
R: (t^3 - 3*t, 8*t - 4*sin(t), 3*t - 1/25*cos(5*t))
R_0: [t^3 - 3*t + 2, 8*t - 4*sin(t) - 2, 3*t - 1/25*cos(5*t) + 101/25]
At this point R_0 contains our final answer.
Section 12.3 Arc Length and Curvature of Space Curves
Arc Length Formula
Here is a formula given in the video assignment 12.3 Q1:
If a smooth curve is defined by \(\mathbf{r}(t) = f(t)\mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}\) on \([a,b]\)
the arc length on the interval is given by
This is the same formula used for parameterized functions, but we now see in this case it represents the integral of the magnitude of the derivative of r of t. In the next code block, we follow along with that same video’s example to see if we can arrive at the same answer in SageMath. Spoiler alert, the output for arc_len, below, is correct.
Finding the Arc Length of a curve in SageMath
t = var('t')
r = vector([2*cos(t), 2 * sin(t), 2*t])
# We are asked to find the arc length from 0 to pi
r_prime = vector(vvf_diff(r, t))
print("r_prime: ", r_prime)
magnitude = r_prime.norm()
print("magnitude: ", magnitude)
arc_len = integrate(magnitude, (t, 0, pi))
print("arc_len: ", arc_len)
def vvf_arc_length(vec, var, a, b):
r_prime = vector(vvf_diff(vec, var))
magnitude = r_prime.norm()
arc_len = integrate(magnitude, (t, a, b))
return arc_len
print("Arc len from function: ", vvf_arc_length(r, t, 0, pi))
r_prime: (-2*sin(t), 2*cos(t), 2)
magnitude: 2*sqrt(abs(cos(t))^2 + abs(sin(t))^2 + 1)
arc_len: 2*sqrt(2)*pi
Arc len from function: 2*sqrt(2)*pi
# Problem 12.3 Q1
t = var('t')
r = vector([5*cos(t), 5*sin(t), 4*t])
print(vvf_arc_length(r, t, 0, 2*pi))
2*sqrt(41)*pi
# Problem 12.3 Q2
t = var('t')
r = vector([4*cos(2*t), 4*sin(2*t), 4*t])
arc_len = vvf_arc_length(r, t, -8, 6)
print(arc_len, " = approx ", round(N(arc_len), 2))
12*sqrt(5)*pi - 8*sqrt(5)*(pi - 4) - 4*sqrt(5)*(pi - 6) = approx 125.22
# Problem 12.3 Q3
t = var('t')
r = vector([e^(4*t) * cos(t), e^(4*t) * sin(t)])
arc_len = vvf_arc_length(r, t, 0, 10)
print(arc_len)
1/4*sqrt(17)*e^40 - 1/4*sqrt(17)
Curvature
The curvature, \(K\), at a point measures how sharply the curve bends or how quickly it changes direction. For a line, curvature is zero, no bend. For a circle, curvature, \(K\) is \(K = \frac{1}{r}\), so it’s greater for smaller circles and more gradual on a larger circle.
There are two formulas for this.
Formula 1
Here, curvature measures how quickly the direction of \(\boldsymbol{T}(t)\) changes with respect to arc length, \(s\)
Here \(d\boldsymbol{T}/dt\) is derivatrive of unit tangent vector value function, \(\boldsymbol{T^{\prime}}(t)\), and \(ds/dt\) is the derivative of the position function, \(r(t)\) which is to say, the velocity function.
Formula 2
Alternative formula:
Evaluating Curvature in SageMath
Below we will implement formula 2 in SageMath:
def vvf_get_curvature(vvf, variable, value):
""" Determines the curvature of the vector valued function vvf for the variable at value. Implements function 2 shown in the avoc
Parameters:
vvf: The vector valued function representing the curve / space curve.
variable: the variable that we'll evaluate at the value given by value
value: the value at which we want to determine curvature.
"""
global t
subst_dict = {variable: value}
r_prime = (vvf_diff(vvf, t)).subs(subst_dict)
r_double_prime = (vvf_diff(vvf, variable, 2)).subs(subst_dict)
numerator = (r_prime.cross_product (r_double_prime)).norm()
denominator = (r_prime.norm())^3
return (numerator/denominator)
# Test it out on an example from the video:
t = var('t')
r = vector([t, t^2/2, t^3/3])
K = vvf_get_curvature(r, t, 1)
print("Curvature, exact: ", K)
print("Curvature, approx: ", N(K))
#print(N(sqrt(2)/3))
Curvature, exact: 1/9*sqrt(6)*sqrt(3)
Curvature, approx: 0.471404520791032
# Problem 12.3 Q 4
t = var('t')
r = vector([-5*t, 3*t^2, -5*t^3])
K = vvf_get_curvature(r, t, 1)
round(N(K), 4)
0.0367
# Problem 12.3 Q 5
t = var('t')
r = vector([-3*t, -4*t^2, 2*t^4])
K = vvf_get_curvature(r, t, -2)
round(N(K), 4)
0.0037
# Problem 12.3 Q 6
t = var('t')
r = vector([2*cos(2*t), 2* sin(2*t), 1*t])
K = vvf_get_curvature(r, t, 0)
round(N(K), 2)
0.47
# Problem 12.3 Q 7
t = var('t')
# Need to add a zero value as a dummy to get cross-product
# in vvf_get_curvature to work.
r = vector([6*cos(t), 5* sin(t), 0])
K = vvf_get_curvature(r, t, (5*pi)/6)
print(K)
80/4107*sqrt(111)
# Problem 12.3 Q 8 can't be solved with vvf_get_curvature because of a divide by zero issue.
# So we'll implement a function using formula one and see if we can arrive at an answer that way.
# NOTE: The answer given is not correct. Note that the associated video for this problem gives
# yet a third function we could use, which is a simplification of formula 2. More work is
# needed based on that video, but the correct vector form for the problem is
# r = vector([x, -3*x^5, 0]), as below.
def vvf_get_curvature_formula1(vvf, variable, value):
unit_tangent_vector = vvf_unit_tangent_vector(vvf, variable)
dT = vvf_diff(unit_tangent_vector, variable)
#print(dT.norm())
numerator = dT.norm().subs({variable: value})
#print("num:", numerator)
ds = vvf_diff(vvf, variable)
denominator = ds.norm().subs({variable: value})
# print("den: ", denominator)
return numerator/denominator
x = var('x')
r = vector([x, -3*x^5, 0])
K = vvf_get_curvature_formula1(r, x, -2)
print("This is not the correct answer. More work is needed: ", K)
This is not the correct answer. More work is needed: 480/3317875201*sqrt(57601)
Section 12.4 Cylindrical and Spherical Coordinate Systems in 3D
Working on Videos first.
Cylindrical Coordinates
In cylindrical cooordinate system a point P in space is represented by \((r, \theta, z)\), where \((r, \theta)\) is the polar representation of a point in the xy plane. As you’d expect, r is the distance from origin, and theta is the angle counter-clockwise from the positive x axis. z is the directed distance up or down from \((r, \theta)\) to the point.
Animation: https://demonstrations.wolfram.com/CylindricalCoordinates
So any point can be viewed as being on that cylinder.
Converting Between Rectangular and Cylyndrical Coordinates in Sage
For converting between coordinate systems.
Cylindrical to Rectangular
Rectangular to Cylindrical
def point_cylindrical_to_rectangular(vec):
l = list(vec)
assert len(l) == 3
r, theta, z = l # unpack
x = r * cos(theta)
y = r * sin(theta)
return vector([x, y, z])
# Video problem -- this solution is correct.
cylindrical = vector([4, pi/3, -2])
rectangular = point_cylindrical_to_rectangular(cylindrical)
print(rectangular)
(2, 2*sqrt(3), -2)
def point_rectangular_to_cylindrical(vec):
l = list(vec)
assert len(l) == 3
x, y, z = l # unpack
r = sqrt(x^2 + y^2)
theta = atan2(y, x)
# Z Stays the same:
z = z
positive = vector([r, theta, z])
negative = vector([-r, theta + pi, z])
return (positive, negative)
rectangular = vector([1, 1, 3])
cylindrical = point_rectangular_to_cylindrical(rectangular)
print(cylindrical)
((sqrt(2), 1/4*pi, 3), (-sqrt(2), 5/4*pi, 3))
Note that for converting equations from rectangular to cylindrical form, it’s impractical to have a set of function that needs to cover all cases, so these need to be done by hand. See 12.4 Video Q2 for details.
# Problem 12.4 Q1 - OK? Problems with entry in Mooc
rectangular = vector([4, -4, -1])
first = point_rectangular_to_cylindrical(rectangular)[0]
print(first)
print(first[1] + pi)
(4*sqrt(2), -1/4*pi, -1)
3/4*pi
# Problem 12.4 Q2, good!
cylindrical = [1, 7*pi/4, -3]
point_cylindrical_to_rectangular(cylindrical)
(1/2*sqrt(2), -1/2*sqrt(2), -3)
# rectangular = vector([2, 4, -4])
rectangular = vector([-5, -1, 5])
pos, neg = point_rectangular_to_cylindrical(rectangular)
checked = point_cylindrical_to_rectangular(pos)
#assert rectangular == checked
checked = point_cylindrical_to_rectangular(neg)
# assert rectangular == checked
print(pos, neg)
(sqrt(26), -pi + arctan(1/5), 5) (-sqrt(26), arctan(1/5), 5)
cylindrical = [5, pi/4, 0]
rectangular = point_cylindrical_to_rectangular(cylindrical)
cylindrical2 = point_rectangular_to_cylindrical(rectangular)
print(rectangular)
print(cylindrical2)
(5/2*sqrt(2), 5/2*sqrt(2), 0)
((5, 1/4*pi, 0), (-5, 5/4*pi, 0))
rectangular = vector([-1, -2, -1])
pos, neg = point_rectangular_to_cylindrical(rectangular)
checked = point_cylindrical_to_rectangular(pos)
# assert rectangular == checked
checked = point_cylindrical_to_rectangular(neg)
assert rectangular == checked
print(pos, neg)
(sqrt(5), -pi + arctan(2), -1) (-sqrt(5), arctan(2), -1)
N(arctan(2))
1.10714871779409
Spherical Coordinates
In spherical coordinates, a point \(P\) is represented by an ordered triple:
\(P = (\rho, \theta, \phi)\)
\(\rho\) is the distance beween the point and origin.
\(\theta\) is the angle counterclockwise from the polar or positive x axis (same as in cylindrical coordinates.
\(\phi\) is the angle between the positive x axis and the point.
A Wolfram demonstration is available: http://demonstrations.wolfram.com/SphericalCoordinates
Converting Between Rectangular Spherical and Rectangular Coordinates
Spherical to Rectangular:
Rectangular to Spherical:
def point_rectangular_to_spherical(rectangular):
x, y, z = rectangular
rho = sqrt(x**2 + y**2 + z**2)
theta = atan2(y, x)
phi = acos(z/rho)
return (rho, theta, phi)
rectangular = [1, sqrt(3), 2]
spherical = point_rectangular_to_spherical(rectangular)
# Agrees with video 12.4 q3
print(spherical)
(2*sqrt(2), 1/3*pi, 1/4*pi)
def point_spherical_to_rectangular(spherical):
rho, theta, phi = spherical
x = rho * sin(phi) * cos(theta)
y = rho * sin(phi) * sin(theta)
z = rho * cos(phi)
return (x,y,z)
spherical = (3, pi/4, 3*pi/4)
rectangular = point_spherical_to_rectangular(spherical)
# Agrees with video 12.4 q3
print(rectangular)
assert rectangular[2] == -(3 * sqrt(2))/2
(3/2, 3/2, -3/2*sqrt(2))
# 12.4 q6 correct
rectangular = (1,3,1)
point_rectangular_to_spherical(rectangular)
(sqrt(11), arctan(3), arccos(1/11*sqrt(11)))
# 12.4 q 8 correct
rectangular = (3, 4, 4)
point_rectangular_to_spherical(rectangular)
(sqrt(41), arctan(4/3), arccos(4/41*sqrt(41)))
# 12.4 q 9 correct
spherical = (2, (7*pi)/6, pi/4)
point_spherical_to_rectangular(spherical)
(-1/2*sqrt(3)*sqrt(2), -1/2*sqrt(2), sqrt(2))
# 12.4 q 10 correct
rectangular = (1, -5, -2)
spherical = list(point_rectangular_to_spherical(rectangular))
# Make second value positive to correct:
spherical[1] = spherical[1] + (2*pi)
print(spherical)
[sqrt(30), 2*pi - arctan(5), arccos(-1/15*sqrt(30))]
# 12.4 Q11
spherical = (2, 5*pi/4, pi/3)
point_spherical_to_rectangular(spherical)
(-1/2*sqrt(3)*sqrt(2), -1/2*sqrt(3)*sqrt(2), 1)